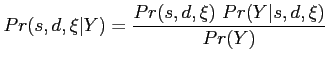Posterior Probability Density

Using Bayes rule, the posteriori probability density of the deformed template given the input image is:

$$Pr(s,d,\xi \vert Y) = \frac{Pr(s,d,\xi) Pr(Y\vert s,d,\xi)}{Pr(Y)}$$ (4.11)

where $Pr(Y)$ is the normalization factor assuring the sum of all probabilities is equal to $1$ . Using Eqs  and , the posterior results in:

$$Pr(s,d,\xi \vert Y) = K_1 \exp\{-\frac{1}{2\sigma^2} [ \sum_{k=1}^N (\xi_k-1)^2 + \Upsilon(\psi^{s,\xi,d},Y) ] \}$$ (4.12)

As the objective is to maximize this probability, we seek to minimize the following objective function with respect to s, $\xi$ , d:

$$\Lambda(\psi^{s,\xi,d},Y) = \sum_{k=1}^N (\xi_k-1)^2 + \Upsilon(\psi^{s,\xi,d},Y)$$ (4.13)

As in the work of Jain et al. [80], this function consists of two terms: a first term that measures the deviation of the deformed template from the prototype, and a second one which describes the fitness of the deformed template to the boundaries of the image.