The likelihood is a measurement of the similarity between the
deformed template and the object(s) present in the image. The
deformable template will be attracted and aligned to the salient
edges in the input image via a directional edge potential field.
For a pixel ![]() in the input image its edge potential can be
defined as:
in the input image its edge potential can be
defined as:
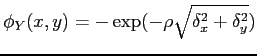 |
(4.8) |
where ![]() is the displacement to the nearest edge
point in the horizontal direction,
is the displacement to the nearest edge
point in the horizontal direction, ![]() in the vertical
direction, and
in the vertical
direction, and ![]() is a smoothing factor which controls the
degree of smoothness of the potential field. This potential is
modified by introducing a directional component relating the
deformed template
is a smoothing factor which controls the
degree of smoothness of the potential field. This potential is
modified by introducing a directional component relating the
deformed template
![]() to the edges of the input image
to the edges of the input image
![]() :
:
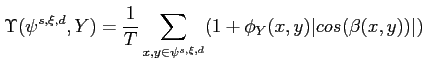 |
(4.9) |
where the summation is over all the pixels on the
deformed template, ![]() is the number of pixels on the template,
is the number of pixels on the template,
![]() is the angle between the tangent of the nearest edge
and the tangent direction of the template at position
is the angle between the tangent of the nearest edge
and the tangent direction of the template at position ![]() , and
the constant
, and
the constant ![]() is added so that
is added so that
![]() is
positive and takes values between 0
and
is
positive and takes values between 0
and ![]() . This definition
requires that the template boundary agrees with the image edges
not only in position, but also in the tangent direction.
Figure
. This definition
requires that the template boundary agrees with the image edges
not only in position, but also in the tangent direction.
Figure ![]() shows three different mammograms
and their respective potential images, where a lighter colour
indicates a higher potential. The vertical and horizontal stripes
comes from those points far away of either a vertical or a
horizontal edge.
shows three different mammograms
and their respective potential images, where a lighter colour
indicates a higher potential. The vertical and horizontal stripes
comes from those points far away of either a vertical or a
horizontal edge.
|
Using the above energy function, the probability density of the likelihood of observing the input image, given the deformations of the template is:
where ![]() is a normalizing constant to ensure that
the above function integrates to
is a normalizing constant to ensure that
the above function integrates to ![]() . The maximum likelihood is
achieved when
. The maximum likelihood is
achieved when
![]() i.e., when the
deformed template
i.e., when the
deformed template
![]() exactly matches the edges in
the input image Y.
exactly matches the edges in
the input image Y.