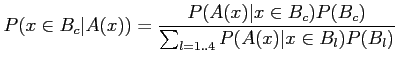 |
(3.6) |
Translating this formula into words, we consider the
probability of a mammogram ![]() , with set of features
, with set of features ![]() , to
belong to the class
, to
belong to the class ![]() as the posterior probability. The prior
is the probability of the mammogram to belong to a class before
any observation of the mammogram. If there were the same number of
cases for each class, the prior would be constant (for four
categories, as is the case for BIRADS classification and hence
as the posterior probability. The prior
is the probability of the mammogram to belong to a class before
any observation of the mammogram. If there were the same number of
cases for each class, the prior would be constant (for four
categories, as is the case for BIRADS classification and hence
![]() , the constant value would be equal to
, the constant value would be equal to ![]() ). Here we
used as the prior probability the number of cases that exists in
the database for each class, divided by the total number of cases.
The likelihood estimation is calculated by using a non-parametric
estimation, which is explained in the next paragraph. Finally, the
evidence includes a normalization factor, needed to ensure that
the sum of posteriors probabilities for each class is equal to
one.
). Here we
used as the prior probability the number of cases that exists in
the database for each class, divided by the total number of cases.
The likelihood estimation is calculated by using a non-parametric
estimation, which is explained in the next paragraph. Finally, the
evidence includes a normalization factor, needed to ensure that
the sum of posteriors probabilities for each class is equal to
one.
Combining the kNN and C![]() classifiers is achieved by a
soft-assign approach where binary (or discrete) classification
results are transformed into continuous values which depict class
membership. For the kNN classifier, the membership value of a
class is proportional to the number of neighbours belonging to
this class. The membership value for each class
classifiers is achieved by a
soft-assign approach where binary (or discrete) classification
results are transformed into continuous values which depict class
membership. For the kNN classifier, the membership value of a
class is proportional to the number of neighbours belonging to
this class. The membership value for each class ![]() will be the
sum of the inverse Euclidean distances between the
will be the
sum of the inverse Euclidean distances between the ![]() neighbouring patterns belonging to that class and the unclassified
pattern:
neighbouring patterns belonging to that class and the unclassified
pattern:
Note that with this definition, a final normalization to
one over all the membership values is required. On the other hand,
in the traditional C![]() decision tree, a new pattern is
classified by using the vote of the different classifiers weighted
by their accuracy. Thus, in order to achieve a membership for each
class, instead of considering the voting criteria we take into
account the result of each classifier. Adding all the results for
the same class and normalizing all the results, the membership for
each class is finally obtained.
decision tree, a new pattern is
classified by using the vote of the different classifiers weighted
by their accuracy. Thus, in order to achieve a membership for each
class, instead of considering the voting criteria we take into
account the result of each classifier. Adding all the results for
the same class and normalizing all the results, the membership for
each class is finally obtained.