Kupinski and Giger [95] compared three region growing approaches: traditional region growing using only grey-level information, region growing using gradient information, and region growing using probability information based on grey-level. The latter approach provided the best results and therefore algorithm a2 is based on that approach.
In the a2 algorithm, the probability of pixel grey-levels
given a partition ![]() is modeled as:
is modeled as:
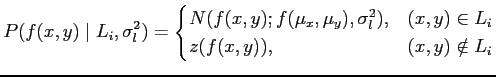 |
(2.6) |
where
![]() is a normal
distribution centred at the seed point grey-level
is a normal
distribution centred at the seed point grey-level
![]() and variance
and variance
![]() , whereas
, whereas ![]() is a function
estimated for each breast using the grey-levels of all its pixels.
This is based on kernel density estimation, which is an extension
of histogram analysis. An Epanechnikov kernel [119]
is used to estimate the pixel distribution. The probability of the
image given a partition
is a function
estimated for each breast using the grey-levels of all its pixels.
This is based on kernel density estimation, which is an extension
of histogram analysis. An Epanechnikov kernel [119]
is used to estimate the pixel distribution. The probability of the
image given a partition ![]() is:
is:
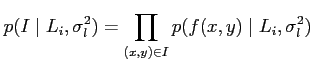 |
(2.7) |
| (2.8) |
Although Kupinski and Giger [95] applied this method to a Region of Interest (RoI) manually selected by an expert, we have slightly modified it with the aim to apply it to whole mammograms. We have automatically placed seeds over the image at high-intensity regions, following an approach proposed to detect micro-calcifications [112].