This algorithm is inspired by recent work of Petrick et
al. [134]. Similar to their other earlier
work [135,136], the algorithm starts by
preprocessing the image using a Density-Weighted Contrast
Enhancement (DWCE) filter. This filter is based on two filtered
images of the original mammogram ![]() :
:
| (2.1) |
where ![]() denotes the convolution operation. This image
is used to define a second multiplication value using another
non-linear filter
denotes the convolution operation. This image
is used to define a second multiplication value using another
non-linear filter ![]() , which is multiplied again by the
weighted contrast of the corresponding pixels:
, which is multiplied again by the
weighted contrast of the corresponding pixels:
| (2.2) |
The main aim of preprocessing is to enhance possible mass lesions in the image. Once the image is filtered, morphological erosion techniques [38] are used to identify local maxima, which are the seeds of a subsequent region growing algorithm which is used to expand them using grey-level and gradient information. The gradient image is obtained using Frequency-Weighted Gaussian (FWG) filtering, which is based on the following decomposition:
| (2.3) |
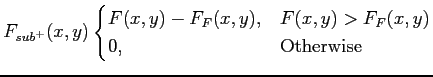 |
(2.4) |
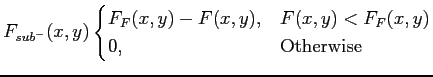 |
(2.5) |
This filtering is repeated twice. The first iteration reduces the gradients within the breast, whilst the second one eliminates gradients in the background. Hence, the result of this decomposition is an enhancement of the contrast between the breast structures and the background. Subsequently, applying a Sobel filter produces the gradient image of the original mammogram with a significant amount of background eliminated. Finally, as a result of this additional information, the region growing algorithm has a limited number of regions to grow.