Xarxes neurals

Return to Artificial Intelligence Lab Notebooks

Autors: Pablo Gay, Beatriz López
Data: 2017-04-03

In [ ]:
# Aquesta linia fa que les grafiques surtin a la llibreta, executar pero no tocar
%matplotlib inline

Material i entorn de treball

  1. Descarregar l'instal·lador de l'entorn de treball Jupyter/WinPython
  2. Executa i espera la descompressió de l'instal·lador.
  3. Instal·lar deixant totes les opcions predeterminades.
    • Per defecte el directori d'instal·lació serà el mateix que el directori de descàrrega.
  4. Obrir la carpeta on acabeu d'instal·lar Jupyter/WinPython, després el directori notebooks.
  5. Descarregueu i descomprimiu el contingut d'aquesta pràctica aquí.
  6. Des del directori d'instal·lació, executar el fitxer Jupyter Notebook.exe
  7. Navegar fins Lab 03 - Deep Learning > Xarxes neurals

Introducció

Les xarxes neurals són un conjunt de neurones artificials interconnectades que utilitzen un model matemàtic de processament de dades basat en una aproximació connexionista per a la computació. Es troben dins del camp de la Intel·ligència Artificial Subsimbòlica. La perspectiva subsimbòlica estudia els mecanismes dels sistemes nerviosos, concretament en aquest cas del cervell, així com la seva estructura, funcionament i característiques lògiques, amb la intenció de dissenyar programes que s’adaptin i generin sistemes capaços de resoldre problemes.

Els mètodes d’aprenentatge basats en xarxes neurals proporcionen una manera robusta per aproximar funcions reals, discretes o vectorials. En particular, per cert tipus de problemes, com els d’interpretar les dades provenint d’un sensor, les xarxes neurals són dels mètodes més efectius coneguts fins al moment.

En el funcionament de les xarxes neurals diferenciem l’etapa d’aprenentatge o entrenament en la que els pesos de les neurones s’ajusten de forma automàtica i l’etapa de simulació en que la xarxa entrenada s’utilitza pel propòsit previst. Així, l’algorisme de “backpropagation” és un dels més usats per entrenar xarxes neurals multicapa feedforward.

Entre les aplicacions podem destacar el identificació de caràcters manuscrits, reconeixement del llenguatge natural, cares, objectes multitud d’aplicacions.

En aquesta pràctica aprendrem a dissenyar xarxes neurals per resoldre problemes concrets mitjançant l’ús de les llibreries Keras.

El primer que caldrà fer serà preparar l'entorn per poder executar totes les comandes, per tant carregarem les llibreries adequades. Començarem amb llibreries ja conegudes de pràctiques anteriors:

  • Numpy per poder treballar amb vectors n-dimensionals fàcilement
  • Pandas per millorar la manipulació de dades.
  • Matplotlib per fer gràfics.
  • Seaborn per millorar els gràfics amb informació estadística.
  • Scikit-learn per les seves llibreries científiques i de processat de dades.
In [ ]:
# Manipulacio de dades
import numpy as np
import pandas as pd

# Plots
import matplotlib.pyplot as plt
import seaborn as sns

# Pre-processat de dades
from sklearn.model_selection import train_test_split

Les llibreries noves que farem servir per treballar amb xarxes neuronals s’anomenen Keras.

Keras van ser desenvolupades inicialment com a part del projecte ONEIROS (Open-ended Neuro-Electronic Intelligent Robot Operating System) per un enginyer de Google i va acabant ser una capa o interfície d'alt nivell per crear xarxes neurals de forma simple amb altres llibreries més potents i de baix nivell per a computació numèrica com Theano i TensorFlow.

Piràmide de llibreries

Qualsevol de les tres llibreries que acabem de mencionar poden ser utilitzades com a mitjà per crear un algorisme de Deep Learning. En el nostre cas, per simplificar la pràctica farem servir directament Keras amb la implementació de baix nivell basada en TensorFlow que és la que ve per defecte amb l'entorn WinPython de la pràctica.

De les llibreries de Keras necessitarem exactament:

  • Sequential: model per a xarxes neuronals on les capes s'organitzen com una llista seqüencial
  • Dense, Activation i Dropout: diferents tipus de capes per les nostres xarxes
  • Adam: optimitzador de pesos de la xarxa
In [ ]:
# Xarxes neurals
from keras.models import Sequential
from keras.layers.core import Dense, Dropout, Activation
from keras.optimizers import Adam
# El primer cop en executar aquestes comandes mostrara un missatge de qui backend fa servir

Classificació d'una XOR

Inicialment les xarxes neuronals no van ser gaire utilitzades degut a que el màxim exponent era el perceptró simple. El perceptró tenia el problema de que només era capaç de classificar problemes linealment separables, és a dir, on les classes poden ser separades amb una recta sense importar com de complexa sigui la funció d'aquesta recta.

Intentem resoldre per exemple la funció XOR (OR exclusiva) fent servir un perceptró simple. La taula de la veritat de la XOR és la següent:

$X_0$ $X_1$ Sortida y
0 0 0
0 1 1
1 0 1
1 1 0

Per tant, carreguem aquestes dades com matrius i vectors:

In [ ]:
# Entrada bidimensional X
X = np.array([[0,0],[0,1],[1,0],[1,1]])
# Entrada unidimensional y
y = np.array([0,1,1,0])

Ara crearem un model de xarxa neuronal mitjançant Keras. Les xarxes neuronals clàssiques, on cada capa està connectada amb la capa anterior i la següent, equivalen a la classe Sequential de Keras. Aquests models seqüencials estan buits i requereixen que afegim les capes necessàries. Farem servir la classe Dense, que representa una capa de neurones on totes les entrades i sortides estan connectades. Concretament especificarem que només volem una neurona (el perceptró) i que aquest perceptró te dues entrades (input_dim=2). Després caldrà afegir una activació per a aquesta capa i ho farem amb la classe Activation, on especificarem que volem que la activació sigui del tipus sigmoïdal (sigmodid). Si intentem buscar equivalències entre aquest model i la següent figura, tenim dues entrades $X_0$ i $X_1$ (input_dim=2) que van a parar a una neurona que representa el perceptró (Dense(1)) i aquesta neurona te una activació sigmoïdal (Activation('sigmoid')).

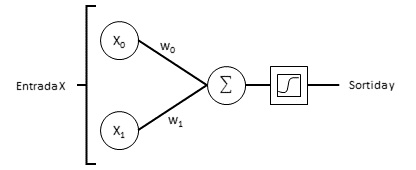Esquema de perceptró de dues entrades Figura: Esquema de perceptró de dues entrades

Si considerem el cas de la funció XOR amb la taula de veritat següent, ens trobem que no existeix cap recta que sigui capaç de classificar tots els casos correctament, això es degut a que aquesta funció no es linealment separable.

In [ ]:
model = Sequential()
model.add(Dense(1, input_dim=2))
model.add(Activation('sigmoid'))

Com hem comentat abans, Keras és una llibreria que fa de capa d'alt nivell de TensorFlow, i per tant un cop hem definit el model caldrà 'compilar-lo' en format TensorFlow per poder executar-lo. Això es realitza amb la funció compile() on per paràmetres li haurem d'especificar quina serà la mesura d'error de la xarxa i quin optimitzador farem servir.

Com a mesura de l'error farem servir l’entropia creuada binaria (binary_crossentropy) ja que tenim una sortida binaria i aquesta mesura contrasta la probabilitat una determinada distribució de probabilitats de la sortida (80% de que sigui 1 i 20% de que sigui 0) amb la real (100% de que sigui un 1, 0% de que sigui 0).

La modificació de pesos en xarxes neurals s'ha realitzat clàssicament mitjançant l'algorisme de backpropagation, però degut a que Keras està preparat per fer deep learning, quan treballem amb xarxes neuronals de dimensions massives aquest algorisme pot ser molt costos computacionalment, per tant, considera que cal algun mitjà d'optimització d'aquest procés. Les opcions per defecte són variacions de mètodes de descens de gradient estocàstics i en aquest cas farem servir Adam.

In [ ]:
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])

Ara que ja tenim el model del nostre perceptró, el podem entrenar amb la comanda fit() on passarem per paràmetre les entrades X, les sortides y, que faci 1000 iteracions per corregir els pesos (nb_epoch), que les dades les introdueixi en l'optimitzador de 4 en 4 (batch_size) i que no ens mostri informació addicional del procés (verbose=0).

In [ ]:
model.fit(X, y, batch_size=4, nb_epoch=1000, verbose=0)

Un cop entrenada la nostre xarxa podem avaluar-la i veure els resultats amb la comanda evaluate().

In [ ]:
score = model.evaluate(X,y)
print('Exactitud de la classificacio:', score[1])

Com podeu veure no hem aconseguit una classificació amb el 100% d'encerts.

Pregunta: Quina avaluació heu obtingut? Comenteu que pot estar passant. Feu servir les gràfiques generades amb les comandes següents per ajudar-vos.

In [ ]:
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)
plt.title('Entrades amb classes reals')
plt.subplot(1, 2, 2)
plt.scatter(X[:, 0], X[:, 1], marker='o', c=model.predict_classes(X))
plt.title('Entrades amb classes predites')

x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5

xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))

Z = model.predict_classes(np.c_[xx.ravel(), yy.ravel()], verbose=0)
Z = Z.reshape(xx.shape)

plt.figure(figsize=(6, 6))
plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, alpha=0.8)
plt.title('Classes reals amb la recta de decisió')

Si volem classificar perfectament les entrades d'una funció XOR necessitarem un perceptró multicapa. Les següents comandes en creant un:

In [ ]:
model = Sequential()
model.add(Dense(5, input_dim=2))
model.add(Activation('sigmoid'))
model.add(Dense(10))
model.add(Activation('sigmoid'))
model.add(Dense(1))
model.add(Activation('sigmoid'))

Pregunta: Descriu l'estructura de xarxa neuronal creant les comandes anteriors. També dibuixa-la fent servir com a guia l’esquema de perceptró de dues entrades mostrat anteriorment.

Si compilem el nou model, l'entrenem i l’avaluem, ara hauríem d'obtenir una exactitud del 100%:

In [ ]:
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X, y, batch_size=4, nb_epoch=10000, verbose=0)

score = model.evaluate(X,y)
print('Exactitud de la classificacio:', score[1])

Pregunta: Feu servir les gràfiques generades amb les comandes següents per comentar perquè la classificació ara si és correcte.

In [ ]:
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)
plt.title('Entrades amb classes reals')
plt.subplot(1, 2, 2)
plt.scatter(X[:, 0], X[:, 1], marker='o', c=model.predict_classes(X))
plt.title('Entrades amb classes predites')

x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5

xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))

Z = model.predict_classes(np.c_[xx.ravel(), yy.ravel()], verbose=0)
Z = Z.reshape(xx.shape)

plt.figure(figsize=(6, 6))
plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, alpha=0.8)
plt.title('Classes reals amb la recta de decisió')

Resistència a la compressió del formigó

Les xarxes neurals no només es poden fer servir en problemes de classificació. Si a la xarxa neural no li posem una funció d'activació i fem servir directament l'agregació de les entrades de l'ultima neurona ponderada amb els pesos de les connexions podem fer-la servir com a sistema de regressió per predir valors d'una variable real.

Per al següent exercici farem servir un dataset del repositori de la UCI Machine Learning Repository, concretament el de força compressiva del formigó.

El formigó és el material més important de la construcció a tot el món. El problema es que la resistència a la compressió d’aquest material és una funció no linear que depèn de molts factors, entre d'altres, de la seva edat i els ingredients que es fan servir per crear-lo. Els ingredients principals solen ser el ciment, escòria d'alt forn, cendres, aigua, superplastificant i àrids.

La descripció del dataset ens explica que les dades són part d'un estudi en condicions de laboratori de la resistència compressiva de formigó (en MegaPascals, MPa) on s'han creat certes barreges d'ingredients i temps de curació. Concretament ens trobem amb 1030 casos diferents composats per 8 variables qualitatives representant les quantitats de cada ingredient i el temps de curació de la mescla i la variable de sortida representant ela pressió de fallida.

Primer de tot fem servir pandas per carregar les dades i descriure-les:

In [ ]:
formigo = pd.read_csv('./Concrete.csv')
formigo.describe()

Per comprovar l'eficàcia de les xarxes neuronals en aquest domini el primer que haurem de fer serà separar els casos que tenim en dos conjunts: un per entrenar i un per comprovar. Ho farem mitjanant la funció train_test_split() de les llibreries de Scikit-learn.

In [ ]:
# Per cada cas, separem els atributs referents a ingredients i temps
# de l'atribut objectiu a predir.
X = formigo.iloc[:, :-1].values
y = formigo.iloc[:, -1].values

# Fem la divisio de train/test
(entrades_train,
 entrades_test,
 classes_train,
 classes_test) = train_test_split(X, y, train_size=0.75)

De la descripció del dataset, ja se’ns ha comentat que es tracta d'un problema no lineal, per tant necessitarem una xarxa neuronal amb perceptrons multicapa com a mínim de tres capes.

Existeix la tendència actual d'anomenar les xarxes neuronals de més de tres capes o més com a Deep Neural Networks degut a que son capces de solucionar problemes n-dimensionals però sense poder donar una explicació analítica dels resultats degut a la perspectiva subsimbólica.

la xarxa neuronal que implementarem està descrita a les següents línies de codi. Recordem que per fer regressió cal que no hi hagi una funció d'activació a la ultima capa. Per millorar els resultats introduirem dos nous tipus de d'activacions/capes: Activació Relu i capa Dropout. Relu es una funció d'activació que serveix com a rectificador, ja que força que tots els valors siguin iguals o superiors a zero, d'aquesta forma aquest valors negatius no es propaguen cap endavant. Dropout és un tipus de capa que no realitza cap funció, només deixa passar les connexions endavant tal i com entren, però amb l'afegit que pot eliminar un cert percentatge de les connexions. Això es fa amb el propòsit d'evitar que el model quedi sobre entrenat amb les dades inicials i després no sigui resistent al soroll. Com que estem tractant un problema de regressió la mesura que farem servir per comprovar l'error de la xarxa neural serà l'error quadràtic mitjà o MSE.

In [ ]:
# Model sequencial
model = Sequential()

# Primera capa: densa de 128 neurones amb 8 entrades
model.add(Dense(128, input_dim=8))
# Afegim una activacio rectificadora relu per eliminar valors inferiors a 0
model.add(Activation('relu'))
# Eliminem el 20% de les conexions seguents per evitar sobreentrenament
model.add(Dropout(0.2))
# Afegim una funcio d'activacio sigmoidal
model.add(Activation('sigmoid'))

# Segona capa: capa oculata densa de 64 neurones amb activacio sigmoidal
model.add(Dense(64))
model.add(Activation('sigmoid'))

# Tercera capa: capa oculata densa de 64 neurones amb activacio sigmoidal
model.add(Dense(64))
model.add(Activation('sigmoid'))

# Capa de sortida: densa amb una unica neurona i sense activació.
model.add(Dense(1))

# Compilem el model
model.compile(loss='mse', optimizer='adam')

# Amb les dades d'entrenament calculem els pesos de la xarxa
model.fit(entrades_train, classes_train, nb_epoch=10, verbose=0)

# Avaluem el model amb les dades de test
score = model.evaluate(entrades_test, classes_test, verbose=0)
print('Test score (MSE):', score)

# Fem un grafic amb els resultats
plt.figure(figsize=(16, 8))
plt.plot(classes_test, label='Real')
plt.plot(model.predict(entrades_test), label='Prediccio')
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.title('Valors reals i predits de la MPa')

Els resultats de l'avaluació no semblen gaire bons. Probablement deu ser que no hem fet servir suficients iteracions en el procés d'entrenament.

Pregunta: Modifica el número d'iteracions en l'entrenament dels pesos de la xarxa fins que obtinguis un resultat que creguis acceptables. Guarda els valors resultants de la puntuació MSE i fes un gràfic amb ells per veure l'evolució de l'error.

Identificació d'imatges

L'exercici final que realitzarem consistirà en crear un sistema capaç de reconèixer dígits escrits a má. Keras facilita la descarrega d'un conjunt de 60000 imatges de 28x28 píxels anomenat MNIST. Aquest dataset d'imatges es fa servir des del 1995 com a conjunt de proves en algorismes de machine learning per comprovar l'eficàcia d'experiments.

Com que cada imatge representarà un dígit, tindrem en les nostres mans un problema de classificació multi classe, concretament 10 classes: 0,1,2,3,4,5,6,7,8 i 9.

Procedim a carregar el dataset. El primer cop pot trigar degut a que cal descarregar les dades.

In [ ]:
# Definim el numero de classes amb les que treballarem
nb_classes = 10

# Per simplicitat, les dades ja venen carregades en format test i train
from keras.datasets import mnist

(X_train, y_train), (X_test, y_test) = mnist.load_data()
print("Estructura original de X_train", X_train.shape)
print("Estructura original de y_train", y_train.shape)

Ara que ja tenim les dades, donem un cop d'ull a les imatges per veure com són:

In [ ]:
# Indiquem a les llibreries Seaborn que no volem la graella a les grafiques
sns.set_style("whitegrid", {'axes.grid' : False})

for i in range(9):
    plt.subplot(3,3,i+1)
    plt.imshow(X_train[i], cmap='gray', interpolation='none')
    plt.title("Classe {}".format(y_train[i]))

Podem veure com les imatges tenen un fons negre i els números estan representats en blanc. El següent pas serà preparar les dades per a que tinguin el format correcte.

Com que les nostres dades d'entrada son imatges però les xarxes neurals nomes accepten vectors, haurem de transformar cada imatge de 28x28 en un vector de 784. A més a més, els píxels de les imatges solen tenir un valor en el rang [0, 255] i per simplificar podem escalar-lo al rang [0, 1].

In [ ]:
# Reshape
X_train = X_train.reshape(60000, 784)
X_test = X_test.reshape(10000, 784)

# Canvi de tipus de dada
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')

# Reescalat
X_train /= 255
X_test /= 255

print("Estructura de la matriu d'entrenament", X_train.shape)
print("Estructura de la matriu de proves", X_test.shape)

Com que tenim un problema de classificació multi classe, caldrà codificar les sortides de la xarxa neuronal. Una aproximació potser fer servir el format one-hot on tindrem 10 sortides binaries a la nostre xarxa però només s'activarà la que indiqui la classe correcte. Per exemple:

0 -> [1, 0, 0, 0, 0, 0, 0, 0, 0]
1 -> [0, 1, 0, 0, 0, 0, 0, 0, 0]
2 -> [0, 0, 1, 0, 0, 0, 0, 0, 0]
etc.
In [ ]:
from keras.utils import np_utils

Y_train = np_utils.to_categorical(y_train, nb_classes)
Y_test = np_utils.to_categorical(y_test, nb_classes)

Ara que ja tenim les entrades i les sortides en el format correcte, podem començar a definir l'estructura de la nostre xarxa neural. Continuarem fent servir un model Sequential amb dues capes ocultes de 512 neurones amb un Dropout del 20% de les connexions i una activació del tipus Relu. La capa de sortida consistirà de 10 neurones (una per cada categoria a classificar) amb una activació Softmax (una generalització de la funció logística).

In [ ]:
# Model sequencial
model = Sequential()

# Primera capa de 512 neurones amb 784 entrades
model.add(Dense(512, input_dim=784))
# Activacio relu
model.add(Activation('relu'))                            
# Eliminem el 20% de les connexions
model.add(Dropout(0.2))

# Segona capa de 512 neurones
model.add(Dense(512))
# Activacio relu
model.add(Activation('relu'))
# Eliminem el 20% de les connexions
model.add(Dropout(0.2))

# Capa de sortida amb 10 neurones i activacio softmax
model.add(Dense(10))
model.add(Activation('softmax'))

Procedirem a compilar el model creat especificant com a optimitzador el mateix que hem fet servir tota l'estona (Adam), que volem veure el resultat en forma d'exactitud i que per calcular l'error faci servir la funció d'entropia creuada categòrica.

Com que tindrem 10 prediccions de distribucions de probabilitat, una per cada dígit (p.ex. 80% de probabilitat que sigui un 3, 10% de que sigui un 8, 2% de que sigui un 9) i la classe que farem servir per entrenar seran distribucions perfectes (100% pel numero que toca, 0% la resta), l'entropia creuada categòrica servirà per diferenciar les distribucions predites amb les indicades per la classe.

In [ ]:
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])

Finalment podem entrenar el model i avaluar-lo. Tingueu en compte com ara només estem fent 4 iteracions per corregir els pesos de forma més o menys ràpida. Si voleu podeu incrementar aquest número però penseu que amb les deep neural networks es treballa amb grans quantitats de dades (ara mateix entreneu amb una matriu de 60000, 784).

In [ ]:
model.fit(X_train, Y_train, batch_size=128, nb_epoch=4, verbose=1)

Avaluarem la xarxa neural com hem fet en els exercicis anteriors amb les dades de test:

In [ ]:
# Mostrem els resultats
score = model.evaluate(X_test, Y_test, verbose=0)
print('Test entropia creuada categorica:', score[0])
print('Test exactitud:                  ', score[1])

Podem aprofitar per generar les prediccions de cada imatge de test i inspeccionar els resultats:

In [ ]:
# Fem les prediccions
predicted_classes = model.predict_classes(X_test)

# Guardar els indexos dels correctes/incorrectes
correct_indices = np.nonzero(predicted_classes == y_test)[0]
incorrect_indices = np.nonzero(predicted_classes != y_test)[0]

# Mostrem exemples de classificacions correctes
plt.figure()
for i, correct in enumerate(correct_indices[:9]):
    plt.subplot(3,3,i+1)
    plt.imshow(X_test[correct].reshape(28,28), cmap='gray', interpolation='none')
    plt.title("Pred {}, Real {}".format(predicted_classes[correct], y_test[correct]))

# Mostrem exemples de classificacions incorrectes
plt.figure()
for i, incorrect in enumerate(incorrect_indices[:9]):
    plt.subplot(3,3,i+1)
    plt.imshow(X_test[incorrect].reshape(28,28), cmap='gray', interpolation='none')
    plt.title("Pred {}, Real {}".format(predicted_classes[incorrect], y_test[incorrect]))

Pregunta: Comenta els resultats obtinguts. Ajudat de les gràfiques generades.

Pregunta: Fen servir Microsoft Paint (o qualsevol altre editor), genereu una imatge de 28x28 amb un dígit i guardeu-lo al directori d'aquest notebook amb el nom numero.png. Aquest bloc de codi carrega la imatge i intenta predir-la. Intenteu fer exemples classificacions correctes i incorrectes.

In [ ]:
import matplotlib.image as img

image = np.dot(img.imread('numero.png'), [0.299, 0.587, 0.114])
plt.imshow(image,cmap='gray', interpolation='none')
image.shape
plt.title('Prediccio: {}'.format(str(model.predict_classes(image.reshape(1, 28*28))[0])))

Que cal entregar

  • Informe de la pràctica en format PDF amb les respostes d'aquesta llibreta.