d1: Pattern Matching Approach

Pattern matching starts by defining a template, in our case, a tumour-like template. The definition of the template is based on the approach of Lai et al. [98], who defined the tumour by three characteristics: brightness contrast, uniform density and circular shape. In our implementation, the template can vary between $3$ and $200$ pixels in diameter. Figure  shows a $5$ -pixel radius template. The circular patch of ones in the centre represents a tumour area having uniform density. The ring of zeros represents the ``don't care" area to account for some of the shape variability. Finally, the outer edge of the template is filled with minus ones to represent the dark background. One of the drawbacks of this algorithm is its poor performance in detecting spiculated masses [98].

Figure 2.5: A tumour-like template for matching with tumours of five pixels in diameter [98].

In contrast with the original work, where the authors used a cross-correlation metric to measure the similarity among the image patches and the template, in this work we used a mutual information based metric. This similarity measure was inspired on the work of Tourassi et al. [179], where they used it to retrieve similar RoIs in a CBIR system. As shown in [129], the results obtained using this probabilistic metric outperforms the ones obtained using the cross-correlation metric.

Given two images A and B, the mutual information is expressed as:

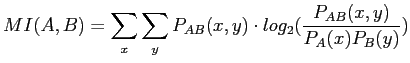$$MI(A,B) = \sum_x{\sum_y{P_{AB}(x,y)\cdot log_2(\frac{P_{AB}(x,y)}{P_A(x)P_B(y)})}}$$ (2.12)

where $P_{AB}(x,y)$ is the joint probability of the two images based on their corresponding pixels values and $P_A(x)$ and $P_B(y)$ are the marginal probabilities of the variables $x$ and $y$ which are the image pixel values, and are obtained from the corresponding normalized histograms. To obtain a compatible template we calculated the mean of all pixels in the breast. Subsequently, in the template, $-1$ 's are replaced with pixels values inferiors to the mean, 0 's with the value of the mean, and $1$ with values superiors to it.