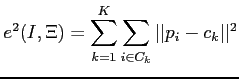c1: k-Means

The popular k-Means clustering algorithm, first proposed by MacQueen [108], is an error-based minimization algorithm, where the minimizing function is the sum of squared error:

$$e^2(I,\Xi) = \sum_{k=1}^{K}\sum_{i\in C_k}\vert\vert p_i-c_k\vert\vert^2$$ (2.9)

In this equation, $\Xi$ represents the partition of the image $I$ , $c_k$ is the centroid of cluster $C_k$ , and $p_i$ is each pattern of the image (each pixel). Two factors have made the k-Means one of the most popular clustering algorithms: it has linear time complexity and it is easy to implement [78].

In mammography, the k-Means algorithm has been applied by Sahiner et al. [155,157], who used the intensity of the pixels as features. Hence, the suspicious regions will be those regions with higher average grey-level. In our implementation the algorithm works with additional features. The aim of the first one is to prevent disconnected regions and, as suggested Jain et al. [78], we use a smoothed version of the original mammogram. In addition, we have included texture features derived from co-occurrence matrices [64] and Laws filters [101]. From co-occurrence matrices, for distances one to five and angles $0^{\circ}$ , $45^{\circ}$ , $90^{\circ}$ and 135$^{\circ}$ , the following statistics have been extracted: contrast, energy, entropy, and homogeneity. The other texture features are based on Laws energy filters of size five.

As has been discussed in Section , the k-Means approach starts by randomly selecting a pre-determined number of seed points. In our experiments, this number can vary from $5$ to $25$ . However, we have observed that best performances are reached when over-segmenting the images. In such cases, the location of a mass is indicated by concentric regions of decreasing intensity.