Algorismes genètics¶
Autors: Pablo Gay, Beatriz López
Data: 2017-05-08
Material i entorn de treball¶
- Descarregar l'instal·lador de l'entorn de treball Jupyter/WinPython
- Executar i esperar la descompressió de l'instal·lador.
- Instal·lar deixant totes les opcions predeterminades.
- Per defecte el directori d'instal·lació serà el mateix que el directori de descàrrega.
- Obrir la carpeta on s'ha instal·lat Jupyter/WinPython, després el directori notebooks.
- Descarregueu i descomprimiu el contingut d'aquesta pràctica dins de la carpeta Notebooks.
- Recomanem crear una subcarpeta AG
- Des del directori d'instal·lació, executar el fitxer Jupyter Notebook.exe
- Navegar fins la carpeta AG i obrir Algorismes-Genetics.ipynb
## Aquesta linia fa que les grafiques surtin a la llibreta, executar pero no tocar
%matplotlib inline
## Fem els imports de les classes necessaries
from ga import BinaryChromosome, RealChromosome, Population
Que cal lliurar¶
Informe de la pràctica en PDF amb les respostes a les qüestions i exercicis, incloent els millors valors trobats, paràmetres corresponents i gràfics quan sigui apropiat.
Introducció¶
Els algorismes genètics emulen el comportament de l’optimització biològica quant a la selecció natural per resoldre problemes d’optimització complexos. Els algorismes genètics treballen sobre una població de solucions (cromosomes), sobre la qual apliquen un conjunt d’operadors: selecció, creuament, i mutació.
En aquesta pràctica aprendrem a utilitzar-los. Farem servir dos tipus de codificació: binària i real, i analitzarem els pros i contres de cadascuna.
Aquesta vegada farem servir la llibreria ga.py creada a propòsit per aquesta pràctica, ja que l'entorn Jupyter/WinPython que hem fet servir fins ara no les incorpora. Aquesta llibreria esta composta per les següents parts:
- BinaryChromosome: Classe que representa un cromosoma on cada gen és un número binari.
- RealChromosome: Classe que representa un cromosoma on cada gen és un número real.
- Population: Conjunt de genomes per evolucionar.
Podeu trobar el codi font aquí
BinaryChromosome¶
A la naturalesa, tot ésser viu té un codi genètic que descriu com és. Aquest codi genètic s'anomenta seqüència d'ADN i és una successió de lletres que representen l'estructura primaria de les molècules que transporten la informació. Aquestes molècules poden ser principalment de quatre tipus Aadenina, Citosina, Guanina i Timina. Quan aquestes molècules s'agrupen en un ordre concret donen lloc a certes característiques, com podria ser tenir els ulls blaus o una predisposició a certes enfermetats.
El cromosoma binari que farem servir intenta portar al domini de la intel·ligència artificial aquest mecanisme. En comptes de fer servir cadenes de quatre molècules diferents (ACGT) fa servir cadenes de 0s i 1s. Les característiques que intenta representar seran paràmetres de funcions i la unió de tots els parametres formaran el cromosoma. Per tant, si volem representar els valors 5 i 2, els valors es transformaran en les cadenes 101 i 010 i el cromosoma final serà 101010.

La classe BinaryChromosome de la llibreria ga encapsula tot aquest comportament.
Per crear un nou cromosoma binari usem la instrucció BinaryChromosome() . Com a resultat ens donara un cromosoma inicialitzat de manera aleatòria d'acord amb les espeficicacions donades. Aquestes especificacions son 4:
- npar: número de variables a optimitzar que contindrá el nostre cromosoma. A l'exemple
npar = 2. - nbits: número de bits amb que es representaran les variables a optimitzar. A l'exemple
nbits = 3, per tant, amb 3 bits podrem representar 8 valors diferents. - lo: valor inferior del rang que poden prendre les variables a optimitzar. A l'exemple
lo = 0. - hi: valor superior del rang que poden prendre les variables a optimitzar. A l'exemple
hi = 7.
Exemple:
# Inicialització d'un nou genoma binari
ch = BinaryChromosome(2, 3, 0, 7)
print(ch)
El cromosoma anterior representara dos variables que tindran valors entre 0 i 7 representats amb 3 bits.
Pregunta 1a: A quins valors reals està representant el cromosoma generat (ch)?
Pregunta 1b: Quants bits caldrien per representar una variable real amb lo = -5 i hi = 5 ?
El mètide decode us proporciona la representació real del cromosoma. La versió actual no permet representar enters.
ch.decode()
Recombinació¶
Per tal d'evolucionar, els cromosomes tenen la capacitat de creuar-se amb altres cromosomes. D'això s'en diu recombinació o crossover.
L'operador de creuament proporcionat en la llibreria ga.py és simple. La recombinació genera un nou cromosoma que conté informació genètica del dos originals. Concretament ho fan decidint un punt aleatori dins de la seqüència de gens. El primer pare proporcionara la seva informació fins aquell punt i el segon a partir d'aquell punt, tal i com indica la següent figura:
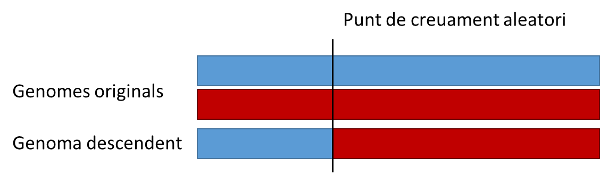
El mètode per fer la recombinació s'anomena crossover() . Es un mètode associat a la classe cromosoma. Per tant qualsevol cromosoma escollit com a pare pot cridar-lo usant entre parèntesis l'identificador del cromosoma parella. Vegeu l'exemple a sota, on el cromosoma ch1 (pare) es creua amb la parella ch2.
# Creem la mare
ch1 = BinaryChromosome(2, 3, 0, 7)
print('Mare', ch1)
# Creem el pare
ch2 = BinaryChromosome(2, 3, 0, 7)
print('Pare', ch2)
# Fem la recombinació
ch3 = ch1.crossover(ch2)
print('Nou ', ch3)
Pregunta 2a: Podries dir en partir de quint punt s'han recombinat els cromosomes?
Pregunta 2b: Què passaria si fessim ch.crossover(ch)?
Mutació¶
El cromosoma binari pot mutar de la mateixa forma que un gen a la natura ho faria. En aquest cas, donada una probabilitat es crearà un número aleatori per cadescun dels gens del cromosoma. Si aquests números aleatòris són inferiors a la probabilitat donada el seu valor s'invertirà: si era un 0 mutarà en un 1 i viceversa. Per provocar la mutació d'un cromosoma caldrà fer servir el mètode mutate() de la següent forma:
ch.mutate(0.5)
print(ch)
On el paràmetre que hem passat (0.5) indica un 50% de probabilitat de que cadescun dels al·lels (valors del cromosoma) pateixi una mutació.
Nota: Normalment la probabilitat de mutació és baixa. Aquí s'ha posat elevada perquè es pugui obtenir un canvi.
Pregunta 3: Quins bits han canviat?
RealChromosome¶
El cromosoma real funciona de la mateixa forma que el cromosoma binari, però en aquest cas en comptes de valors binaris, els valors seran valors reals i representaran directament les variables a optimitzar. En aquest cas disposem de la instrucció RealChromosome():
# Inicialització d'un nou genoma real
ch = RealChromosome(5, -1, 1)
print(ch)
RealGenome només necessita 3 entrades:
- npar: número de variables que el cromosoma ha de representar. A l'exemple
npar = 5. - lo: valor inferior del rang que poden prendre les variables. A l'exemple
lo = -1. - hi: valor superior del rang que poden prendre les variables. A l'exemple
hi = 1.
Recombinació¶
La recombinació també es farà mitjançant el mètode crossover(). D'una forma similar al genoma binari, es decideix un punt aleatori dins del cromosoma. El primer cromosoma proporcionarà els parametres fins aquell punt i el segon cromosoma a partir d'aquell punt.
# Creem la mare
ch1 = RealChromosome(5, -1, 1)
print('Mare', ch1)
# Creem el pare
ch2 = RealChromosome(5, -1, 1)
print('Pare', ch2)
# Fem la recombinació
ch3 = ch1.crossover(ch2)
print('Nou ', ch3)
Mutació¶
La mutació en el cas del cromosoma reals també és similar a la binaria, però en aquest cas donada una probabilitat de mutació, si un gen la sobrepassa, prendrà un valor nou aleatori dins del rang permés. Igual que abans es farà mitjançant el mètode mutate().
# Mutació d'un genoma real amb un 50% de probabilitat
ch.mutate(0.5)
print(ch)
Funció fitness¶
La funció de fitness mesura la qualitat de la solució representada i es defineix sobre el cromosoma. Aquesta funció dependrà sempre del problema.
Per exemple, en el problema del viatjant de comerç les sol·lucións podrien ser l'ordre en que el comerçiant visita les ciutats. El fitness de les solucions seria la distància recorreguda o el temps trigat en fer el camí.
Un altre exemple, si estem creant un model d'intel·ligència artificial (com per exemple una xarxa neural), una solució podria ser el conjunt de paràmetres que optimitzen el model (en una xarxa neural: iteracions, número de capes ocultes, neurones per capes, etc.) i la funció de fitness l'error del model.
La llibreria ga està pensada per poder definir funcions de fitness totalment genèriques fent servir funcions de Python. Una funció de python segueix la segënt estructura: la paraula clau def, el nom de la funció i entre parèntesis els paràmetres. A més a més, ha de retornar un valor que representara el fitness fent servir la comanda return.
A continuació se us presenta un exemple de codificació per a la funció $f(x) = |x| - x*cos(x)$:
import numpy as np
def funcio_a_maximitzar(x):
return np.abs(x)-x*np.cos(x)
print( funcio_a_maximitzar(3) )
Podeu fer servir la documentació online de la llibreria numèrica Numpy per si necessiteu trobar funcions matemàtiques específiques com $cos$ (que en aquesta llibreria està definit en radiants).
A efectes didàcits, es pot visualitsar la funció utilitzant la llibreria matplotlib, com s'il·lustra a continuació.
import matplotlib.pyplot as plt
t = np.arange(-5., 5., 0.2) # generem punts x des de -5 fins a 5, amb intervals de 0.2
plt.plot(t, funcio_a_maximitzar(t))
Algorisme genètic¶
El diagrama de flux d'un algorisme genètic segons (Haupt & Haupt 2004) es mostra a la següent figura.
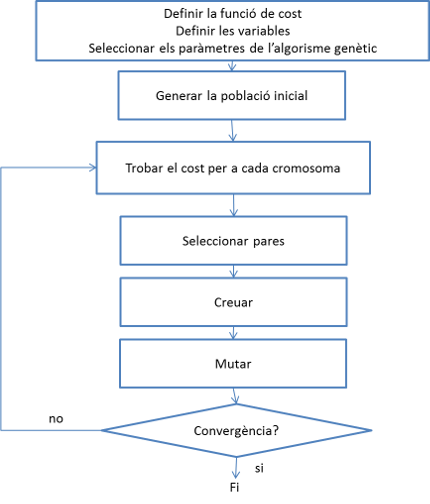
Per facilitar-vos la tasca, se us proporciona un exemple d'implementació en ga.py. En particular, es tracta d'un algorisme que implementa:
- Un mètode de selecció per truncació
- Un operador de recombinació de punt únic, com el que s'ha explicat abans
- Un operador de mutació, com el que s'ha explicat abans
D'una iteració (o era) a una altra, la població que passa (mètode de re-inserció) segueix un mètode elitista (els pares que són seleccionats i els seus descendents, passen a la següent generació).
Configuració¶
Cal que definiu primer
- la funció de cost (fitness),
- definir les variables (com es representa un cromosoma),
- definir els paràmetres de l'algorisme genètic (probabilitat de mutació mutation_prob, retain_prob percentatge de cromosomes que són seleccionats)
retain_prob = 0.5 # El 50% de la població passara a la seguent era
mutation_prob = 0.01 # El 10% dels gens patiran mutacions
fitness = funcio_a_maximitzar # nom de la funcio que hem definit abans
Generar la població inicial¶
Primer usem l'inscrucció Population per crear la població d'acord amb els paràmetres de configuració
poblacio = Population(retain_prob, mutation_prob, fitness)
A continiuació cal inicialitzar la població amb la quantitat de cromosomes que desitgem.
Per això, Population té el mètode addChromosome que serveix per afegir un nou cromosoma a la població. addChromosome només requereix com a paràmetre el cromosoma a incloure a la població. Per tant caldrà primer definir com seran. A sota trobareu un exemple en el cas de treballar amb cromosomes binaris; en el cas voler fer servir genomes reals només caldria canviar el constructor.
npar = 1 # numero de parametres que contindra el cromosoma.
nbits = 10 # numero de bits que representaran cada parametre
lo = -5 # limit inferior del rang de valors dels parametres
hi = 5 # limit superior del rang de valors dels parametres
tamany_poblacio = 20 # quantitat de genomes a incloure a la poblacio
for _ in range(tamany_poblacio):
ch = BinaryChromosome(npar, nbits, lo, hi)
print('Chromosoma ', ch, ch.decode())
poblacio.addChromosome(ch)
Procés¶
La classe Pupulation té un segon mètode, evolve, que encapsula tots els blocs del diagrama de flux des de Trobar el cost per a cada cromosoma fins a Convergencia?. Té un paràmetre explícit (cal mencionar el nom quan es passa el paràmetre): max_eras, numero màxim de vegades que es fara evolucionar la població.
Com a resultat ens retornarà un vector on cada posició del vector contindrà informació sobre quin son els millors cromosomes (best_genes), el millor fitness (best_fitness) i el fitness mig de la població (avg_fitness).
info = poblacio.evolve(max_eras=100)
Info es una estructura de dades que conté la informació del resultat de totes les iteracions, com es mostra a dalt.
Si volem recuperar i decodificar el millor cromosoma trobat, podem fer-ho mitjançant l'instrucció següent.
print(info[99]['best_genes'].decode())
En el cas que volguem mostrar l'evolució gràficament, podem fer servir les comandes que hem apres en pràctiques anteriors. La llibreria matplotlib ens permetrà fer plots i veure els resultats.
plt.plot(range(len(info)), [era['best_fitness'] for era in info])
plt.plot(range(len(info)), [era['avg_fitness'] for era in info])
plt.title('Evolució del fitness. Millor: {}'.format(info[-1]['best_genes']))
plt.legend(['millor','mitjana'])
Pregunta 4: Quin a estat el millor fitness trobat? A quin valor correspon?
Exemple complet¶
A continuació es mostra un exemple complet.
def funcio_a_maximitzar(x):
return np.abs(x)-x*np.cos(x)
retain_prob = 0.5
mutation_prob = 0.01
fitness = funcio_a_maximitzar
numero_eras = 100
npar = 1
nbits = 10
lo = -5
hi = 5
tamany_poblacio = 20
poblacio = Population(retain_prob, mutation_prob, fitness)
for _ in range(tamany_poblacio):
ch = BinaryChromosome(npar, nbits, lo, hi)
print('Chromosoma ', ch, ch.decode())
poblacio.addChromosome(ch)
info = poblacio.evolve(max_eras=numero_eras)
plt.plot(range(len(info)), [era['best_fitness'] for era in info])
plt.plot(range(len(info)), [era['avg_fitness'] for era in info])
plt.title('Evolució del fitness. Millor: {}'.format(info[-1]['best_genes']))
plt.legend(['millor','mitjana'])
print(info[99]['best_genes'].decode())
Exercici 1: Repeteix el proces des que es genera la població i edita els paràmetres de la creació dels cromosomes per obtenir un millor resultat. Quin son els millors resultats ara?
Consideracions de minimització¶
Suposem ara que es vol trobar el valor òptim que minimitza la funció $f(x) = |x| + cos(x)$
def funcio_a_minimitzar(x):
return np.abs(x)+np.cos(x)
Atenent que els algorismes genètics troben valors màxims, caldrà reconsiderar la funció:
$f(x) = \frac{1}{|x| + cos(x)}$
def funcio_a_maximitzar(x):
return 1/ (np.abs(x)+np.cos(x))
Veiem quines implicacions té gràficament:
t = np.arange(-5., 5., 0.2) # generem punts x des de -5 fins a 5, amb intervals de 0.2
plt.plot(t, funcio_a_minimitzar(t), t, funcio_a_maximitzar(t))
plt.legend(['mini','max'])
Per algunes funcions $f(.)$ que volguem minitzar, caldrà tenir en compte possibles valors de la funció que retornin 0, i causin valors indesitjables a la inversa (i.e., dividir per 0). Per la qual cosa, una bona pràctica pot ser usar com a inversa la següent funció: $\frac{1}{1+f(.)}$
Exercici 2a: Utilitzeu aquesta plantilla exemple per obtenir els valors de x que fan mínim la funció:
$f(\overrightarrow{x}) = \sum_{i=1}^{N}|x_i^2|$
per $-100 \leq x_i \leq 100$, $N = 3$
Tingeu en compte $\overrightarrow{x}$ és un vector de dimensió $N$, per la qual cosa, s'estaran trobant diversos $x_i$.
Exercici 2b: Editeu la plantilla de codi per fer servir genomes reals i repetiu les minimitzacions per les mateixes funcions. Caldrà incloure les modificacions a l'informe.
Exercici 3a: Utilitzeu aquesta plantilla per obtenir els valors de x que fan mínim la funció:
$f(\overrightarrow{x}) = \sum_{i=1}^{N}|x_i| - 10 cos(\sqrt{|10x_i|})$
per $-99999 \leq x_i \leq 99999$, $N = 5$
Exercici 3b: Editeu la plantilla de codi per fer servir genomes reals i repetiu les minimitzacions per les mateixes funcions. Caldrà incloure les modificacions a l'informe.